Guide to Elections ACT audit sample performance calculator
This document explains the design and the use of the spreadsheet “ACT EC audit sample
performance calculator.xlsx”
Inputs and outputs
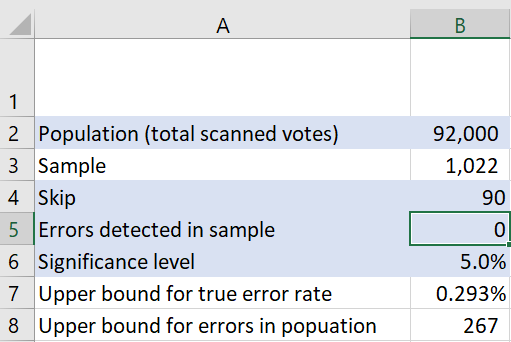
The screenshot below shows the key cel s of the spreadsheet with the row and column indicatives
Input cells are shaded in blue. Column A holds the labels for the values in column B. Inputs are
entered in cells B2, B4, B5 and B6. These inputs are described below.
•
Population (B2): This is the total number of scanned bal ot papers. The population can
either be for the entire election, or if desired the population for an electorate can be
entered to produce outputs for an electorate. The population size is specified as an input to
allow the sensitivity of the sampling scheme to be explored for variations in the population
size.
•
Skip (B4): This specifies the sampling rate, for example if a value of 90 is entered it
represents a sampling scheme where 1 in 90 ballots are selected for audit. Skip is a sampling
term to il ustrate selecting a random starting point, then skipping ahead 90 bal ots for the
next selection. It can also be referred to as “inverse sampling rate”, the inverse of 90 is 1/90
which is the rate at which the population is sampled. The population size divided by the skip
gives the sample size, which is shown in the spreadsheet in cell B3.
•
Errors detected in sample (B5): This is the number of erroneous ballot papers detected
within the audit sample. The conclusions drawn about the error rate will obviously depend
on how many erroneous bal ots are detected within the audit sample. Changing this value
shows how large the true error rate may be when a certain number of errors are detected
within the audit sample.
•
Significance level (B6): This is the level of statistical significance for which an error rate is
produced. Typical y, values of 5% or 1% are used, but any value greater than 0% and less
than 100% can be used.
The outputs are shown in cells B3, B7 and B8. The outputs are described below.
•
Sample (B3): This is the audit sample size. It is calculated by dividing the population size
(cell B2) by the sampling skip (cell B4).
•
Upper bound for true error rate (B7): This is an upper bound for the rate of erroneous
ballot papers in the population, for the significance level specified in cell B6. It gives the
upper end of a one-sided confidence interval. If the significance level is 5%, then there is
only a 5% chance that the error rate in the population is greater than the upper bound,
which can also be expressed as 95% confidence that the error rate in the population lies
between 0 and the upper bound.
•
Upper bound for errors in population (B8): This is an upper bound for the number of
erroneous ballot papers in the population, for the significance level specified in cell B6. It is
calculated by multiplying the error rate in cell B7 by the population size in cell B2.
Cells used for calculation
Columns E and F are where the calculations of probability are performed. The values in columns E
and F are referred to by the formula in cell B7 to choose the appropriate error rate. Columns E and F
can be hidden to make the spreadsheet look simpler and less confusing, the spreadsheet has been
delivered to elections ACT with the columns unhidden to make the design transparent.
Method used
The spreadsheet calculates a one-sided confidence interval. In most applications where confidence
intervals are used, they are two-sided confidence intervals, with both a lower and upper bound.
Usually the confidence interval is centered on the point estimate (the estimated error rate) and the
confidence interval shows the range of plausible values (for the specified significance level)
accounting for the sampling variability.
One-sided confidence intervals have been used as the last several audits have detected no errors in
the audit sample. This means a confidence interval cannot be centered around the point estimate of
zero – the true error rate cannot be any smal er than zero. So a one-sided confidence interval only
have one bound, in this case an upper bound with the lower bound always set to zero.
The spreadsheet uses the Clopper-Pearson method, also known as the “exact method” to calculate
binomial distribution probabilities and the final confidence interval. Often an approximate method
is used for confidence intervals based on the normal distribution, but this approximation is not
appropriate to use when the error rate is very smal , and wil not produce good results when there
are zero errors detected in the audit sample.
Column F sequentially lists a set of error rate values, starting at 2% and reducing in steps of 0.001%
to a minimum value of 0.001%. The values in column F represent the true rate of erroneous bal ots
in the population. Column E then calculates the probability that a Binomial distribution Bin(n,p)
returns a value of k or smaller; where n is the audit sample size (cell B3), p is the probability of an
error (the corresponding value in column F), and k is the number of errors found in the audit sample
(cell B5). That is, column E gives the probability of selecting a sample that has k or fewer erroneous
forms, if the error rate in the population is as specified in column F. The formula in cell B7 searches
column E for the probability that is closest to the significance level specified in cell B6, and selects
the corresponding value from column F as the upper bound.
The choice of filling column F with values between 0.001% and 2% in steps of 0.001% means that cell
B7 can only return values in this range, and only to a precision of 0.001%. The spreadsheet wil not
return a value in cell B7 if the upper bound lies outside this range, which can happen if a smal
sample size (from a large sampling skip) or a very small significance level is specified. This
shortcoming can be overcome by replacing the values in column F, for example from 10% to 0.005%
in steps of 0.005%. Alternatively, column F could range from 10% to 0.001% in steps of 0.001% but
would need to extend down to row 10001, with column E similarly fil ed down to row 10001, and the
formula in cell B7 would need to be updated from =VLOOKUP($B$6,$E$2:$F$2001,2,TRUE) to
=VLOOKUP($B$6,$E$2:$F$10001,2,TRUE).
